Path Homotopy in the Context of Fuel Optimal Trajectories

09 Jul, 2025

It's not uncommon to see the term "homotopy" used in papers when solving for minimum fuel spacecraft trajectories. While I've used the process before, I've never really understood the theory from which it originates nor what the concept broadly is in any thorough manner. I thus decided to teach myself rudimentary algebraic topology and, in doing so, have notably expanded my understanding of not only optimal control problems, but also many other fundamental math concepts. Note well that this is written from the perspective of one familiar with dynamics and control methods rather than algebraic topology--thus, many details of those areas are brushed over to focus on the basics of homotopies.

Spacecraft Trajectory Optimization

To lay down the context for this, and the motivation for using path homotopy, we'll start at the problem of interest: generating optimal trajectories for spacecraft. Often, this is approached from the perspective of knowing where you are now and where you want to be at some time later. "Where you are" and "where you want to be" are not just positions, but a full states that include velocity, thereby fully defining your orbits. Time may or may not be given explicitly--this changes the boundaries of interest in this problem, but still the problem remains tractable.

This can be treated then as a boundary value problem--the equations of motion (differential equations) are known and the boundaries (start and end conditions) are known, thus it is solvable as such. It is not this which is of interest per se, but the fact that the minimum fuel solution to this, as defined by minimizing,

J_{1} = \int_{t_{0}}^{t_{f}} | u (t) | d t

where $u$ is the acceleration of the vehicle, is very hard to converge to. I'm going to gloss over many of the intricacies of the calculus of variations that defines such problems, but this forms into a control law which is inherently discontinuous and holds regions where the control is not defined. There is, however, another formulation of the minimum effort problem that instead minimizes the total energy expended rather than the total fuel expended,

J_{2} = \int_{t_{0}}^{t_{f}} u (t)^{2} d t

To again gloss over the details of this, the minimum energy solution is significantly easier to converge to. It has no discontinuities and no regions where control is undefined.

Thus, we have a problem: we can solve for one trajectory between our states but we desire another.

Relevant Algebraic Topology

On a dit souvent que la géométrie est l’art de bien raisonner sur des figures mal faites - Henri Poincaré¹

If you have a familiarity with topology you likely can already guess where this is going. For those of us that don't, I shall again lay out the basics--this time of path homotopy instead of optimal control.

To explain path homotopy we must first explain homotopy, which requires before that an explanation of topological spaces. A topological space is defined as a set of subsets of a set (we shall notate this $(X, 𝒯)$ , where $X$ is the parent set and $𝒯$ is a set of subsets within $X$ ) that satisfy 3 axioms:

$\emptyset, X \in 𝒯$ ;
$\cup 𝒯_{i} \in 𝒯$ ;
$\cap 𝒯_{i} \in 𝒯$ .

Translated to English,

Both the empty set and $X$ are within $𝒯$ ;
The union of any two elements of $𝒯$ is within $𝒯$ ;
The intersection of any number of elements of $𝒯$ is within $𝒯$ .

I'll now describe two topological spaces, notated for brevity as $X$ and $Y$ . We now have two maps (functions),

p, q : X \to Y

which take something in $X$ and return something in $Y$ . These maps are homoptic if $p$ can be continuously deformed into $q$ , written as $p ≃ q$ . This is notated as such,

H : X \times [0, 1] \to Y

where $H$ is a homotopy--a continuous family of maps from $X$ to $Y$ that satisfies $H (x, 0) = p (x)$ and $H (x, 1) = q (x)$ .

While this may appear abstruse, it is simply a concise notation that describes maps that exist somewhere between $p$ and $q$ as a function of the second input to $H$ , $[0, 1]$ . It is this knowledge we build upon as we proceed into the topic of path homotopies.

We will now take some new $p$ and $q$ have them instead intake some value from $0$ to $1$ and output some 2-dimensional coordinate,

p, q : [0, 1] \to X : X \subseteq ℝ^{2}

You can now think of $p$ and $q$ as lines drawn on a piece of paper. We will now enforce a condition on these two maps--they must start and end at the same points--that is, $p (0) = q (0) = x_{0}$ and $p (1) = q (1) = x_{1}$ . If a homotopy exists between $p$ and $q$ now, and their endpoints are fixed throughout the homotopy, they are declared homotopic relative to their endpoints, and we can define the following path homotopy between them,

F : [0, 1] \times [0, 1] \to X

where $F (s, 0) = p (s)$ , $F (s, 1) = q (s)$ , $F (0, t) = x_{0}$ , and $F (1, t) = x_{1}$ .

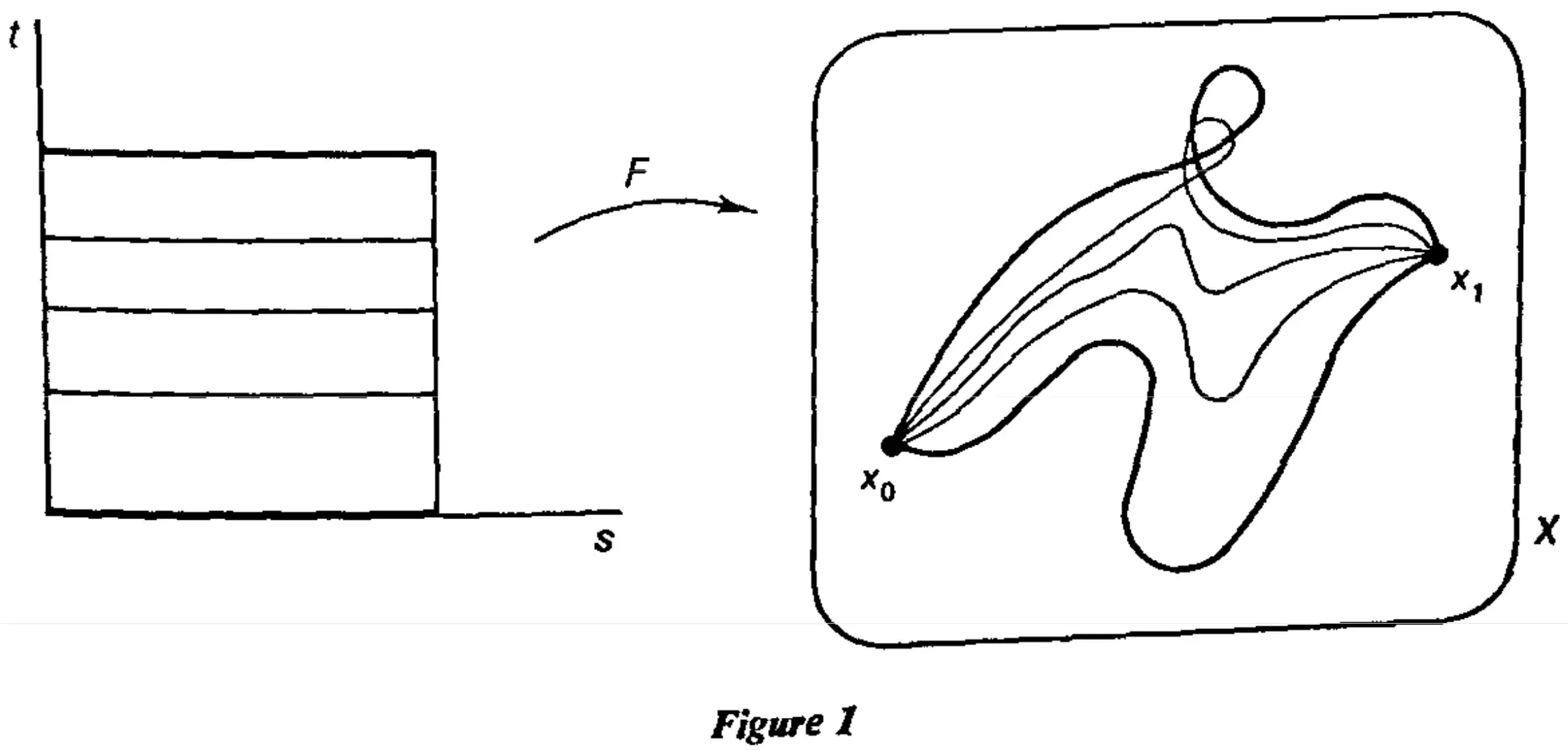Image of the family of paths F between p and q A neat example of this type of homotopy from Munkres². The left side of this square is $x_{0}$ , the right side is $x_{1}$ , the top is $q (s)$ , and the bottom is $p (s)$ . The horizontal lines within are the intermediate deformations between $p$ and $q$ .

We now have a tool $F (s, t)$ that can take a single path connecting two endpoints and deform it into another path connecting the same endpoints. It is with this which we solve the impasse from the first section.

Applying $F (s, t)$ to Spacecraft Trajectories

It is chiefly important to think about the trajectories that minimize $J_{1}$ and $J_{2}$ (which I will refer to as $y_{1}$ and $y_{2}$ from here on out) as paths themselves expressed as such,

y_{1}, y_{2} : [0, 1] \to X : X \subseteq ℝ^{6}

We treat the time of the first state as $0$ and the second state as $1$ , thereby normalizing time. Let us also assume the initial and final states we desire are again $x_{0}$ and $x_{1}$ . We can now express the path homotopy between them as,

H : [0, 1] \times [0, 1] \to X

where $H (s, 0) = y_{1}$ , $H (s, 1) = y_{2}$ , $H (0, t) = x_{0}$ , and $H (1, t) = x_{1}$ . The notation here is a bit confusing since traditionally toplogists seem to use $t$ for the movement between paths³--in contrast to the usage of $t$ for time in dynamics (here represented with $s$ instead).

There are many mechanizations of this, but all are built upon embedding the term $t$ into the cost function, and therein the derived control, of the system. From there, the solution to $y_{2}$ is found and fed back into the solver as an initial guess for values of $t$ steadily approaching $y_{1}$ . A fairly straightforward example that simply inserts $u^{t} : t \in [1, 2]$ into the cost function results in the following control law (found by $\frac{\partial ℋ}{\partial u} = 0$ ),

u : ℝ^{3} \times ℝ \to ℝ^{3} : λ \times t \mapsto - (‖ λ ‖ / t)^{1 / (t - 1)} \hat{λ}

where $λ$ is the costate associated with the control in the dynamics.

Appendix: Behaviors of Different Minimum Effort Control Laws

I want to write this because when introduced to these cost functions, they seemed no different to me. What minimizes $| u |$ should minimize $u^{2}$ . What I failed to think about was the--often implied rather than explicitly written--time dependence of $u$ . While, yes, minimizing $| u |$ and $u^{2}$ gives the same result, minimizing $| u (t) |$ and $u (t)^{2}$ does not.

As an example, let's say our craft must perform a burn and has two options--one, a strong impulse of $u (1) = 4$ followed by $u (2) = 0$ , and one, a smoother, softer burn of $u (1) = 2.5$ and $u (2) = 2.5$ . We will denote the former as $A$ and the latter as $B$ . Let us say for this example that, since $B$ is weaker initially, it must utilize more control later to reach its end point. Thus, we have the two cost function evaluations:

	$A$	$B$
$J_{1}$	4	5
$J_{2}$	16	12.5

It is apparent that, while $A$ expends less fuel (minimizing $J_{1}$ ), the squaring of the term in $J_{2}$ heavily penalizes its large control authority. Herein lies the behavioral difference of the control resulting from these two cost functions-- $J_{1}$ is inherently a bang-off-bang controller, favoring large, binary control authorities, whereas $J_{2}$ produces softer, smoother movements, minimizing the square of its control.

Appendix: Henri Poincaré's Thoughts on the Communication of Mathematics

The start of this quote was at the start of a chapter in Armstrong's book. While at first it's simply amusing, upon further reading, I found it quite thought provoking and wanted to include it in full here.

On a dit souvent que la géométrie est l’art de bien raisonner sur des figures mal faites. Ce n’est pas là une boutade, c’est une vérité qui mérite qu’on y réfléchisse. Mais qu’est-ce qu’une figure mal faite? C’est celle que peut exécuter le dessinateur maladroit dont nous parlions tout à l’heure; il altère les proportions plus ou moins grossièrement; ses lignes droites ont des zigzags inquiétants; ses cercles présentent des bosses disgracieuses; tout cela ne fait rien, cela ne troublera nullement le géomètre, cela ne l’empêchera pas de bien raisonner. Mais il ne faut pas que l’artiste inexpérimenté représente une courbe fermée par une courbe ouverte, trois lignes qui se coupent en un même point par trois lignes qui n’aient aucun point commun, une surface trouée par une surface sans trou. Alors on ne pourrait plus se servir de sa figure et le raisonnement deviendrait impossible.⁴

(Roughly translated) It has often been said that geometry is the art of reasoning well on poorly made figures. This is not a joke, it's a truth that deserves to be thought about. But what is a badly made figure? This is the one that can be executed by the clumsy cartoonist we were talking about earlier; he alters the proportions more or less crudely; his straight lines have disturbing zigzags; his circles have unsightly bumps; all this does nothing, it will not disturb the surveyor, it will not prevent him from reasoning well. But the inexperienced artist must not represent a curve closed by an open curve, three lines that cut at the same point by three lines that have no common point, a surface pierced by a surface without a hole. Then we could no longer use our figure and reasoning would become impossible.

Basic Topology, M.A. Armstrong ↩
Topology: A First Course, J.R. Munkres ↩
A Concise Course in Algebraic Topology, J.P. May ↩
Pourquoi L'espace a Trois Dimensions, H. Poincaré↩