
This is an overview of one half of the optical navigation system I've developed for Georgia Tech eXperimental Rocketry (GTXR).
Aboard GTXR rockets are either Arducams or NoIR camera modules--simple, commerical-of-the-shelf (COTS) cameras connected to a Raspberry Pi. These provide a very cheap, simple sensor that can be used for absolute attitude determination.
To achieve full attitude knowledge, two vectors to known bodies are needed. Classically, this was used for TRIAD attitude determination[0]. The sounding rockets launched by GTXR are suborbital, so the two most notable bodies in view of a simple camera system would be the sun and Earth.
Horizon detection is a common task performed in a wide variety of optical attitude determination sytems. When looking at these systems, even in different environments, something becomes obvious--the enviornment is not changing. That is, a spacecraft performing horizon-based optical navigation will always be dealing with a lit limb of an airless body (or at least it should be), a maritime application will always be dealing with the flat line gradient between sea and sky, and so on and so forth. Thus, the methods used for these applications can be tuned for their specific signature. To my knowledge, this is how most horizon sensing and estimation is done (see Note A below).
The issue with this is that on a suborbital rocket, the environment is not a constant. That is, the signature we're looking for (the horizon) is changing. Near ground level, we distinguish the horizion by the relatively sharp, flat gradient between the ground color (tan for the desert) the sky color (usually a form of blue). As altitude increases, the horizon is then distinguished by the haziness between the darker sky above and the bright ground below, where now a slight curve can be seen. Finally, as we get to our highest altitudes, the horizon can be distinguished by the same bright haze between the blackness of space and the bright colors of the Earth where the seen curvature is much more prominent.

Thus, the question arises--how can we detect this changing signature in a unified manner? Obviously, we could employ multiple methods that switch at different altitudes, each targeting a specific signature, but that would be clumsy and inelegant. After much analysis and many attempts of isolating the horizon at different altitudes, a solution presented itself: there is often a notable gradient in saturation between the sky and the ground. This is the constant signature that RANGER looks for to estimate the horizon across the entire regime of flight.

As a preface to the logic flow of RANGER, I want to note that this algorithm does not strive to be high precision. In opposition to industry horizon-based spacecraft OPNAV, RANGER is only trying to give a relatively close estimate of the attitude of the rocket relative to a spherical Earth. RANGER would be ill-suited for premier NASA missions. It is meant to work robustly under unideal conditions with consumer hardware--often the case for collegiate high powered rocketry.
Firstly, the horizon in the saturation scene is very prominent. There is also a myriad of smaller detail we don't care about. Thus, the first thing we do is apply a low-pass filter to the saturation image to rid it of these unwanted details.
After the filter is applied, we then take the gradients in the scene.
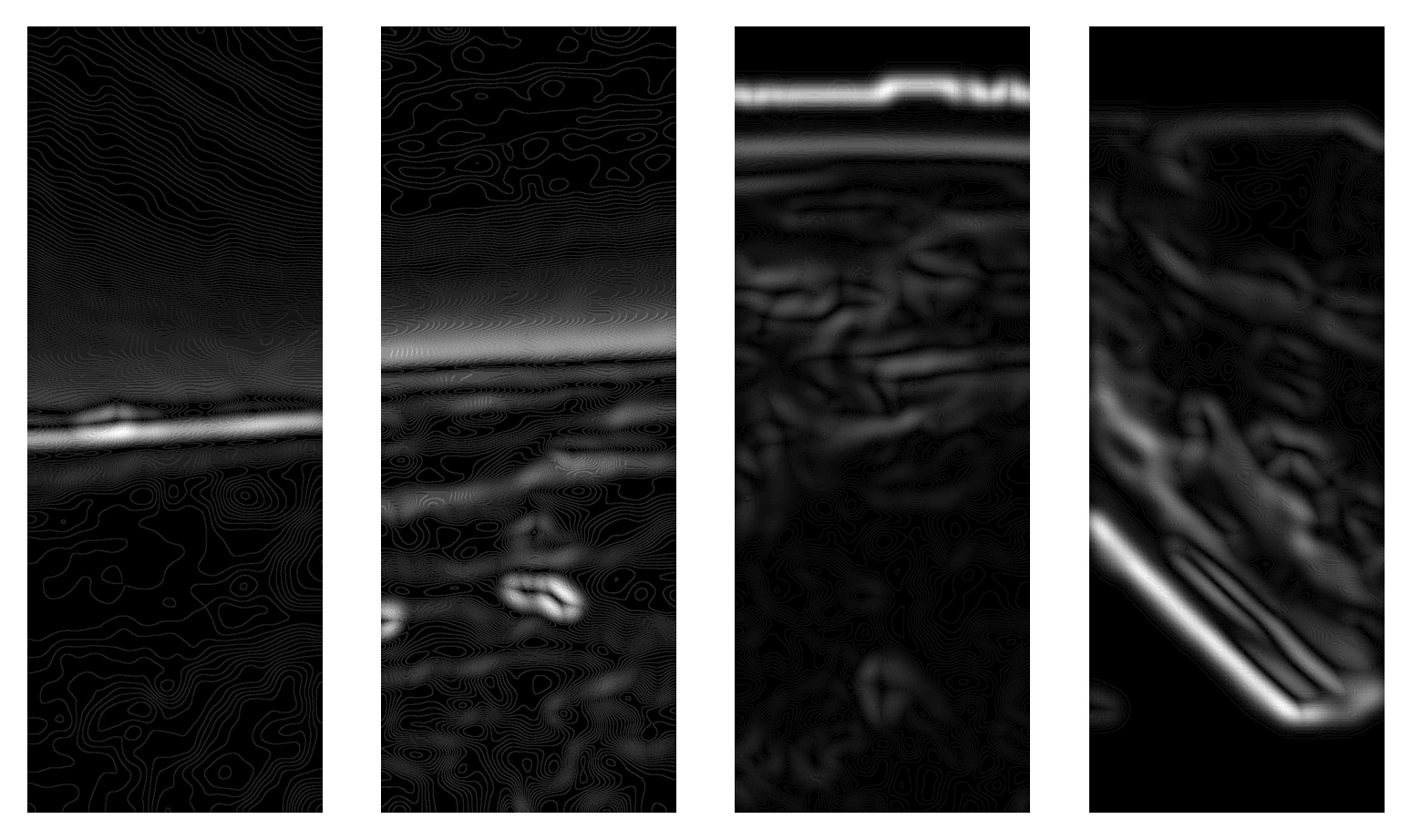
There is still much unwanted information in these gradients. Luckily, we still have much more information from our sensor to utilize! We know the horizon cannot lie in the blackness of space and we know the signature we're looking for is a byproduct of a generally highly saturated atmosphere. Thus, we can mask our image from thresholds of these values to further rid the image of information we don't care about. Further, we know the horizon has strong gradients relative to others in the image. So, we can take a threshold of this gradient mask above a certain value (experimentally found to be 45% of the maximum brightness value in the image) to further rid the image of unwanted information.

From the above image, we can see the horizon line clear as day (ha).
From here, a light low-pass filter is applied to ensure all of the masked gradients are self-connected before applying cv2.bwconncomp to segment the individual blobs in the image. RANGER sorts through these blobs to look for the largest that is within an area window (i.e., larger than random information but smaller than an overexposed bright spot) and greater than a diagonal length threshold (i.e., line-like in shape, as opposed to a 'denser' object like a circle). If a blob in the scene passes these, then RANGER concludes a horizon has been found and proceeds to estimating the rocket's pose from this.

The horizon blobs found from the main image processing section of the code are incredibly useful, but imprecise. How do you quantify the orientation of such an odd object to recover attitude from it? Rather than doing it directly with this blob, we choose to approximate the blob with a line. A large simplification, but generally accurate enough in testing.

From this line, we can very simply quantify its orientation and position in the camera frame. Of note, we choose to compute the angle between it and horizontal in the frame (and ensuring the Earth is 'down'--see Note B below) as well as the distance between the center of the frame and a point normal to the line from the center point.
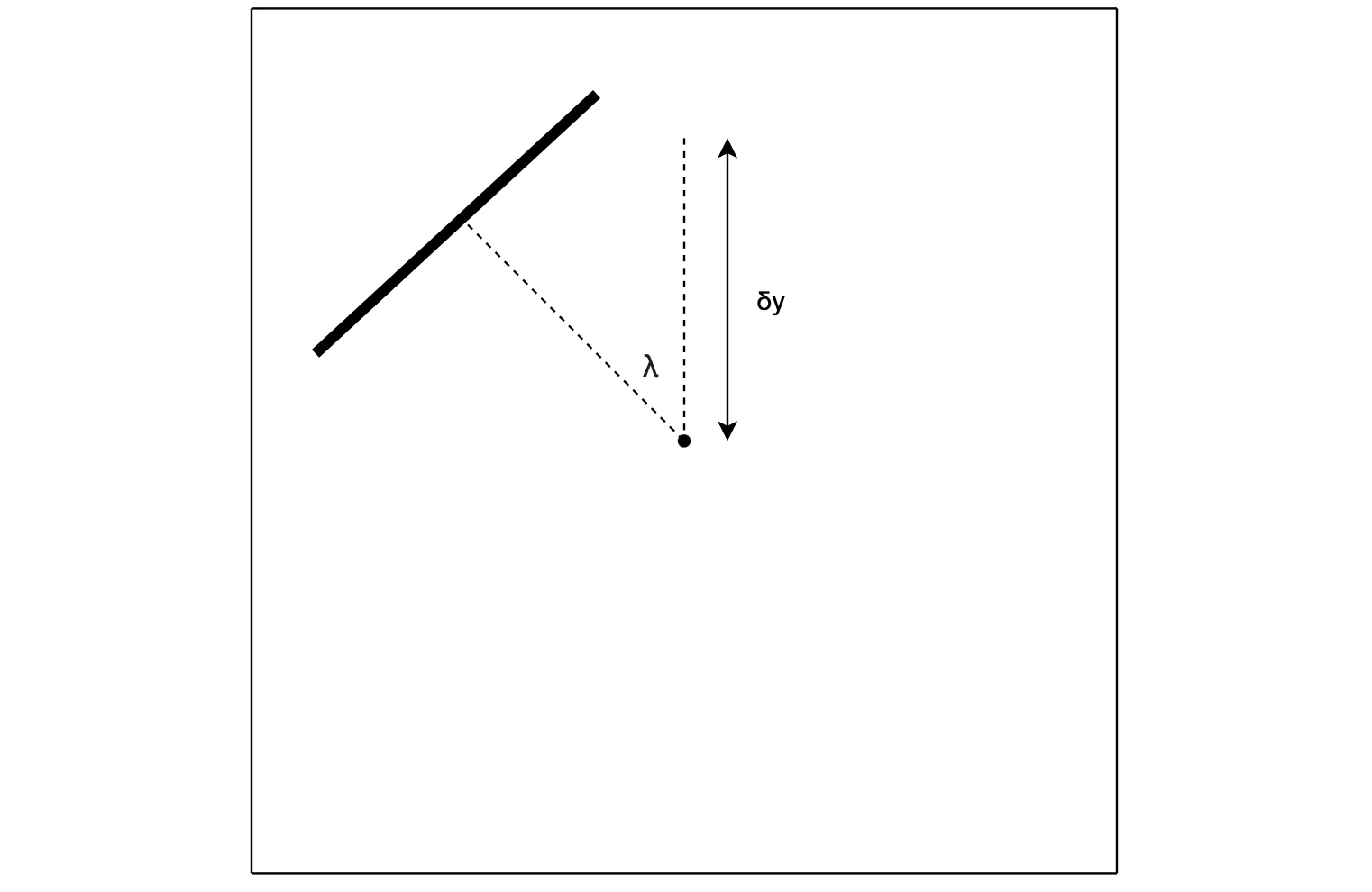
The yaw of the rocket with respect to the horizon can be computed directly from \(\lambda\) in the above scene, but the pitch indicated from the \(\delta y\) term is more elusive. Very simply, the difference in pixel values multiplied by the instantaneous field of view (IFOV) of the camera will yield the real world angle between center of the frame and the line in the figure--but remember, the whole point of this is that we're trying to make a method of doing this for a rocket that's changing altitudes. The horizon, in zenith pointed flight, will begin to sink under the center of the frame as the rocket gains altitude.
RANGER accounts for this by pulling altitude estimates from the flight computer and comparing them against a look up table of pixel offsets. This offset is simply subtracted from the pixel length \(\delta y\) and we are left with the pixel offset due to pitching. This value is what is finally muiltiplied by the IFOV to yield the angular pitch of the rocket in the real world.
With these two angles, two direction cosine matrices (DCMs) can be made to rotate a nominal nadir vector (+\(y\) in the camera frame) to the actual nadir vector at the time the image was taken.
$$ \begin{bmatrix}x\\\ y\\\ z\end{bmatrix} = R_{x}(IFOV\delta y)R_{z}(\lambda)\begin{bmatrix}0\\\ 1\\\ 0\end{bmatrix} $$
This completes the logic of RANGER (satuRAtioN Gradient horizon EstimatoR) and the vector is given to the main flight computer to use its in Kalman filter.
While this is generally true, while writing this post I actually stumbled upon a method[1] that is seemingly agnostic to the signature of interest. It basically works by selecting a line position and orientation which segments the image into two portions. The line is manuevered to maximize the mahalanobis distance between the colorspaces of both segments. That is, it looks for a line that makes the colors on each side of the line as different as possible.
I haven't implemented this myself, but in theory it would be pretty adaptable in the way that RANGER is meant to be. I plan to try this out just to see how it performs--it's a very clever and interesting method of doing this.
This was initially a very problematic thing to check for--and not something I even thought about. Of course we know where the Earth is! In fact, the flight computer does not inherently know where the Earth is. Thus, it must be calculated.
The final method I settled on for this was a hybrid approach--if the sun is detected by THRASHER for a given frame, RANGER automatically places the Earth on the other side of the horizon. If THRASHER does not see the sun in the frame, then RANGER centroids the red channel of the original color image. The red channel of any given frame should mostly be dominated by the Earth--the atmosphere isn't that red, nor is space. Thus, the centroid of this channel should exist on the side of the horizon that holds the Earth.
This method is not without issues--of note, when going through a regime of particular haziness in zenith pointed flight, the centroid approaches the center of the frame. Thus, if the horizon is near the center, it can end up placing the Earth on the wrong side of the horizon. This seems to be an edge case, so presently this implementation is acceptable.
[0] A Passive System for Determining the Attitude of a Satellite ^
[1] Vision-Guided Flight Stability and Autonomy for Micro Air Vehicles ^